Matrices

Matrices is a set of real or imaginary number that arranged in the form of a rectangular array(rectangualr box) . array like A[m][n] where m represent row and n represent column is known as m*n or m by n matrix.

We can also represent m by n matrix as A=[a_pk]_m*n
where a₁₁,a₁₂,a₁₃,a₁₄ etc are elements of matrix and element a_pk are p^throw and k^th column element of metrix.

Type of Matrices in Algebra

Square matrix
Row matrix
Column matrix
Scalar matrix
Diagonal matrix
Unit matrix
Null matrix
Upper triangular matrix
Lower triangular matrix

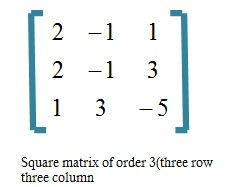
Square matrix :A square matrix is a matrix which number of row is equal to the number of columns. example of square matrix

Row matrix :A row matrix is a matrix that have only one row.it also known as row vector. Example of row matrix A=[3 5 -3 -1] order of row matrix is represented by 1*n only one row with multiple column.

Column matrix :A column matrix is a matrix that have only one column.

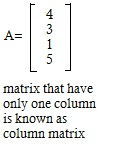
Scalar matrix : A square matrix is called a scalar matrix if a_pk=0 for all p ≠ k and a_pk=C for all p , C≠0
means leading diagonal elements are equal(not zero) and other element are zero

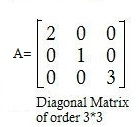
Diagonal matrix : If all the elements, except those in the leading diagonal of square matrix are zero then matrix known as diagonal matrix. a_pk=0 for all p≠k

Unit matrix :Square matrix is known as unit matrix if leading diagonal elements of square matrix is 1 and other element is equal to zero

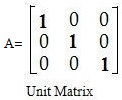
Null matrix : Matrix is called null matrix or zero matrix if all elements of metrix are zero.

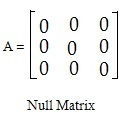
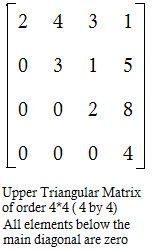
Upper triangular matrix :A square matrix is called a Upper triangular matrix if all elements below the leading diagonal are zero. a_pk=0 for all p >k

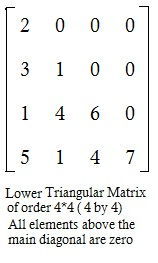
Lower triangular matrix : A square matrix is called a Lower triangular matrix if all elements above the leading diagonal are zero. a_pk=0 for all p <k